How to: technical indicators with Rust and Binance

In this tutorial, we will learn how to implement technical indicators with Rust using data from Binance. The aim of this tutorial is to be a fun exercise for people who are starting out with Rust and want to see a practical example of writing basic functions.

First, we will implement algorithms for the following technical indicators: Simple Moving Average (SMA), Exponential Moving Average (EMA), Moving Average Convergence Divergence (MACD), Bollinger Bands (BOLL), and the Relative Strength Index (RSI). Then, we will download historical data from the Binance API and use that to apply our algorithms.

We will also look at writing tests for our functions, that way we don’t have to run the program and download data to test if our functions are working properly.

We are going to go through the indicators step by step and show how the algorithm can be implemented and then use real-world data to look at the results.

My GitHub repository has the full project here.

I also have tutorials on other aspects of the Binance API:

• Binance API crypto transaction with Rust: how to
• Easily connect to Binance WebSocket streams with Rust

If you are interested in how to visualize technical indicators with Rust I have a quick article about that here: Plot Candles and SMA with Rust: learn how to.

Project set up

First, let’s create the “technical indicators with Rust and Binance” project using cargo: cargo new rust-binance-technical-indicators-tutorial.

Next, we’ll add the relevant dependencies to the Cargo.toml file in the project’s root directory:

[package]
name = "rust-binance-technical-indicators-tutorial"
version = "0.1.0"
edition = "2021"

# See more keys and their definitions at https://doc.rust-lang.org/cargo/reference/manifest.html

[dependencies]
tokio = { version= "1", features = ["full"] }
reqwest = { version = "0.11", features = ["json"] }
serde = { version = "1.0", features = ["derive"] }
serde_json = "1.0"

Links to the crate pages:

• tokio: An event-driven, non-blocking I/O platform for writing asynchronous I/O backed applications.
• reqwest: higher level HTTP client library.
• serde: A generic serialization/deserialization framework.
• serde_json: A JSON serialization file format.

Why technical indicators

Why would we want to implement technical indicators? There are a number of reasons why implementing technical indicators with Rust for the Binance API or in general, could be useful. For example, if we want to implement our own version of the Binance trading dashboards including technical indicators. The Binance trading dashboard has a number of technical indicators that we will look at in this tutorial.

Traders use these technical indicators also in automatic trading strategies. In other words, when writing a trading bot.

Lastly, it is educational to implement algorithms when learning a programming language. Furthermore, if we can look at real-world examples and use real-world data, that is even better!

Initial file set up

We will have three main files:

• main.rs: our main program logic.
• statistics.rs: here we will implement our statistics or technical indicator algorithms.
• test_statistics.rs: in this file we will implement tests for our statistics functions.

Let’s create an empty statistics.rs file now in the same directory as main.rs. Then let’s add the test_statistics.rs file there as well, with the following contents:

#[cfg(test)]
mod test_statistics {
    use super::super::statistics::*;
}

Here on line 3, we pull everything from the statistics module into scope for easy access to the functions.

Test code will only be compiled when the command cargo test is used when using the following annotations #[cfg(test)] for our module block and #[test] for each individual test function.

Finally, let’s at these modules to main.rs:

mod statistics;

#[cfg(test)]
mod test_statistics;

fn main() {
    println!("Hello, world!");
}

Getting Binance historic crypto price data

In this first section, we are going to briefly look at how to get historic price data for cryptocurrencies on Binance. We will use the Binance API, and the Kline/Candlestick endpoint specifically.

Get a HTTP client instance

To connect to the Binance API with Rust we need an HTTP client that can send requests. Let’s write a function that builds a client using reqwest. Create a file called utils.rs and add the following code:

use reqwest::Client;

static APP_USER_AGENT: &str = concat!(env!("CARGO_PKG_NAME"), "/", env!("CARGO_PKG_VERSION"));

pub fn get_client() -> Client {
    let client = Client::builder()
        .user_agent(APP_USER_AGENT)
        .build()
        .unwrap();

    client
}

Here we simply build a basic Client instance and return it. We give the agent a name containing our project name and version, taken from what is in Cargo.toml.

We have to add the module to main.rs now too:

mod statistics;
mod utils;
#[cfg(test)]
mod test_statistics;

Let’s modify the rest of main.rs as well to create an instance of the HTTP client there. While we are at it let’s make the main function async:

mod statistics;
#[cfg(test)]
mod test_statistics;
mod utils;

#[tokio::main]
async fn main() {
    let client = utils::get_client();
}

Binance historic price data model

Now we can send a request to the Binance API to get price data. We do not need an account for this as “market data” is publicly available through the API. However, before we start sending requests let’s write a struct that we can deserialize the data to.

Please note that the data structure for Klines as listed in the Binance API documentation shows an array of values instead of a JSON dictionary:

[
  [
    1499040000000,      // Open time
    "0.01634790",       // Open
    "0.80000000",       // High
    "0.01575800",       // Low
    "0.01577100",       // Close
    "148976.11427815",  // Volume
    1499644799999,      // Close time
    "2434.19055334",    // Quote asset volume
    308,                // Number of trades
    "1756.87402397",    // Taker buy base asset volume
    "28.46694368",      // Taker buy quote asset volume
    "17928899.62484339" // Ignore.
  ]
]

So, how can we map this array of values to a struct? We actually don’t have to worry about it, because serde takes care of this for us. As long as we put the fields in the struct in the correct order.

Let’s add a new file called models.rs, which will contain our data model:

use serde::{de, Deserialize, Deserializer, Serialize};

#[derive(Debug, Deserialize, Serialize, Clone)]
pub struct KlineData {
    pub open_time: i64,
    #[serde(deserialize_with = "de_float_from_str")]
    pub open: f64,
    #[serde(deserialize_with = "de_float_from_str")]
    pub high: f64,
    #[serde(deserialize_with = "de_float_from_str")]
    pub low: f64,
    #[serde(deserialize_with = "de_float_from_str")]
    pub close: f64,
    #[serde(deserialize_with = "de_float_from_str")]
    pub volume: f64,
    pub close_time: i64,
    #[serde(deserialize_with = "de_float_from_str")]
    pub quote_asset_volume: f64,
    pub number_of_trades: usize,
    #[serde(deserialize_with = "de_float_from_str")]
    pub take_buy_base_asset_volume: f64,
    #[serde(deserialize_with = "de_float_from_str")]
    pub take_buy_quote_asset_volume: f64,
    #[serde(deserialize_with = "de_float_from_str")]
    pub ignore: f64,
}

pub fn de_float_from_str<'a, D>(deserializer: D) -> Result<f64, D::Error>
where
    D: Deserializer<'a>,
{
    let str_val = String::deserialize(deserializer)?;
    str_val.parse::<f64>().map_err(de::Error::custom)
}

The only thing of note is the [serde(deserialize_with = "de_float_from_str")] annotation for certain fields. The floats in the Binance API response are actual strings, so we have to parse them in this way with the function on lines 28-34.

As mentioned earlier, we will use the Klines/Candlesticks endpoint: https://api.binance.com/api/v3/klines.

Writing the function for downloading Cryptocurrency historic price data from Binance

Our function,called get_klines, sends a GET request to the /klines endpoint and then deserializes the JSON in the response.

Let’s put this code in a new file called binance.rs:

use crate::models;
use reqwest::{Client, StatusCode};

static BINANCE_URL: &str = "https://api.binance.com/api/v3";

pub async fn get_klines(
    client: Client,
    interval: &str,
    symbol: &str,
    limit: u32
) -> Option<Vec<models::KlineData>> {
    let req_url = format!(
        "{}/klines?symbol={}&interval={}&limit={}",
        BINANCE_URL, symbol, interval, limit
    );

    println!("request url: {}", &req_url);

    let result = client.get(&req_url).send().await.unwrap();

    let data: Vec<models::KlineData> = match result.status() {
        StatusCode::OK => {
            serde_json::from_value::<Vec<models::KlineData>>(result.json().await.unwrap()).unwrap()
        }
        _ => {
            println!("StatusCode: {}", result.status());
            println!("Message: {:?}", result.text().await);
            return None;
        }
    };

    Some(data)
}

First, we bring some items from reqwest and our own module models into scope. Then we define the base URL for the Binance API.

Our function takes four parameters:

• A Client object instance. We pass in an object instead of creating a new one in the function so that we can make use of the connection pool. For faster subsequent connections.
• The interval is a string indicating what time interval the data should be mapped to. For example, sending 1d as the value results in each data point representing a whole day. We can also get data points for each hour, 2 hours etc. the full listing is below:

m -> minutes; h -> hours; d -> days; w -> weeks; M -> months

1m
3m
5m
15m
30m
1h
2h
4h
6h
8h
12h
1d
3d
1w
1M

• A symbol string. This is the coin pair to retrieve the data for. For example, BTCUSDT, ETHUSDT, ETHBTC, etc.
• Finally, a limit to the amount of data point to retrieve. Default is 500, max is 1000.

We use these parameters to add a query string to the Binance API endpoint URL on line 12-15, and then use the client object to send a request on line 19.

On line 21 and 22 we are making sure the response is successful by matching result.status to StatusCode::OK. If so, we deserialize result.json() using serde_json::from_value, using our data structure KlineData from the models module as the type to deserialize to.

The end result is a Vec<KlineData> which we return from the function.

If the request fails we print the status code and the raw response in text form, then return None, on lines 26-28.

Download and display coin price data

Finally, let’s call this function and print some data to the terminal by updating main.rs:

mod binance;
mod models;
mod statistics;
#[cfg(test)]
mod test_statistics;
mod utils;

#[tokio::main]
async fn main() {
    let client = utils::get_client();
    let result = binance::get_klines(client.clone(), "1d", "BTCUSDT", 500).await;

    let kline_data = match result {
        Some(kline_data) => kline_data,
        _ => {
            panic!("Something went wrong.");
        }
    };
    println!("first result: {:?}", kline_data[0]);
}

Here we call get_klines from the binance module we wrote earlier using the HTTP client instance, 1 day interval (1d), and BTCUSDT as the symbol, meaning price data for buying/selling BTC for USDT.

Then some error handling on lines 13-18. And finally, we print the debug information of the first item in the Vec.

Running the program with cargo run --release should give a result like this in the terminal:

 Finished release [optimized] target(s) in 12.39s
 Running `target/release/rust-binance-technical-indicators-tutorial`
request url: https://api.binance.com/api/v3/klines?symbol=BTCUSDT&interval=1d
first result: KlineData { open_time: 1597449600000, open: 11760.55, high: 11980.0, low: 11680.0, close: 11852.4, volume: 56237.90505, close_time: 1597535999999, quote_asset_volume: 667446824.0641296, number_of_trades: 1018956, take_buy_base_asset_volume: 27303.966321, take_buy_quote_asset_volume: 324138943.4177591, ignore: 0.0 }

Now that we have some real-world Binance data let’s start writing the Rust code for the technical indicators.

Implementing Simple Moving Average (SMA)

In this section, let us implement one of the easiest ones: the simple moving average (SMA). The SMA calculates the average prices for a certain time window. For example, for the last 26 days. This gives a smoother view of the price movement and a possible trend over the period.

Often, people will compare multiple SMA lines to discover a change in trend, usually an SMA with a longer time window versus an SMA with a shorter time period. An example would be a 200 day SMA vs a 25 day SMA.

The Simple Moving Average formula

The formula is quite simple:

   

Where is all the values that fall within the time window and is the length of the time window. For example, for 20 days there would be 20 values divided by 20.

What we are going to implement is a function that takes the following parameters:

1. A data set, or list, of floating point values.
2. The window size (number of values to use) for calculating the average.

Writing the Simple Moving Average tests

Let’s start by writing a simple test in test_statistics.rs function that will verify that the results from our SMA function are correct:

#[cfg(test)]
mod test_statistics {
    use super::super::statistics::*;

    #[test]
    fn test_simple_moving_average() {
        let data_set = vec![5.0, 6.0, 4.0, 2.0];

        // test with window size 2
        let result = simple_moving_average(&data_set, 2).unwrap();
        assert_eq!(3, result.len());
        assert_eq!(vec![5.5, 5.0, 3.0], result);

        // test with window size 3
        let result = simple_moving_average(&data_set, 3).unwrap();
        assert_eq!(2, result.len());
        assert_eq!(vec![5.0, 4.0], result);

        // test with window size 4
        let result = simple_moving_average(&data_set, 4).unwrap();
        assert_eq!(1, result.len());
        assert_eq!(vec![4.25], result);

        // test with window size bigger than data size, should return None
        let result = simple_moving_average(&data_set, 5);
        assert_eq!(None, result);
    }
}

The test is straightforward. We initialize a small data set on line 7. Then call the function we have not written yet: simple_moving_average. We will write this function in the next section. However, we can already see what the function signature will look like from this test setup. That is, we pass in a reference to the Vec of floating point numbers, and a number to indicate the number of values to use to calculate the average.

Then we see that the result is supposed to be a Vec of length 3, which is shorter than the input data set. It will become clear why that is when we write the function.

Next, we test with different window sizes.

Finally, we test that None is returned when the window size is bigger than the dataset size on lines 24 – 26.

Writing the Simple Moving Average algorithm

In this section, we will write the actual code for this algorithm. What we are going to do is write a loop that takes a slice of the data set the size of the given window for each loop.

Here is the code for this algorithm:

pub fn simple_moving_average(data_set: &Vec<f64>, window_size: usize) -> Option<Vec<f64>> {
    if window_size > data_set.len() {
        return None;
    }

    let mut result: Vec<f64> = Vec::new();
    let mut window_start = 0;
    while window_start + window_size <= data_set.len() {
        let window_end = window_start + window_size;
        let data_slice = &data_set[window_start..window_end];
        let sum: f64 = data_slice.iter().sum();
        let average = sum / window_size as f64;
        result.push(average);
        window_start += 1;
    }

    Some(result)
}

The function takes two parameters a reference to a list of floating-point numbers: data_set, and the number of items to use for calculating the average: window_size. Our function can return a list of floating-point numbers or None. That’s why we return Option<Vec<f64>>, instead of just Vec<f64>.

At first, the function checks to see if window_size is bigger than the data set size, if so, the function returns None.

Then on line 6, we create an empty Vec, which is to be filled by our for-loop. On line 7 we set the window_start variable, which tracks where the moving average calculation starts from. This window_start variable is updated every loop to move the window along the data set.

We then loop while the window start + window size doesn’t exceed the size of the data set.

Every loop we take a slice of the data set that fits in the window size and calculate the average value from that slice on lines 10-11. Then we push the value into the result object.

At the end of the loop, we move the window start 1 position up.

After the loop is done, we return the result.

Executing Simple Moving Average tests

Now that the algorithm is implemented in a function we can run the tests to verify that we have done a good job. Let’s run the tests using the cargo test command. The result should look something like this:

running 1 test
test test_statistics::test_statistics::test_simple_moving_average ... ok

test result: ok. 1 passed; 0 failed; 0 ignored; 0 measured; 0 filtered out; finished in 0.00s

Simple Moving Average with real data

Let’s use Binance KLines/Candlestick data to test our first of the technical indicators written in Rust. We will calculate the SMA for a window of 26 days.

First, we will create a Vec<f64> using the data from Binance and then we can pass that as a data set to the SMA function:

let price_data: Vec<f64> = kline_data.iter().rev().take(100).map(|f| f.close).collect();
let result = statistics::simple_moving_average(&price_data, 26);

let sma_data = match result {
    Some(data) => data,
    _ => panic!("Calculating SMA failed"),
};

println!("SMA: {:?}", sma_data);

Here on line 21, we get the Vec of f64 based on the close prices for the period. We reverse the order of the vec with rev() and then take(100) to take the 100 latest values.

Then we call our simple_moving_average function on line 22.

Finally, after checking for a valid result, we print the debug string for sma_data. After running the program it should look something like this:

SMA: [49371.27115384616, 49610.10769230769, 49847.6103846154, 50131.32538461539, 50379.590000000004, 50528.90615384615, 50726.535769230766, 51113.86192307692, 51507.097692307696, 51924.79153846154, 52286.81846153846, 52767.234615384616, 53231.66269230769, 53585.01884615385, 53913.80115384616, 54438.49807692308, 54823.30461538463, 55370.10269230771, 56076.9703846154, 56724.447692307716, 57249.48769230772, 57795.07653846156, 58350.48076923078, 59025.531923076924, 59732.19961538462, 60104.220384615386, 60296.15384615386, 60440.501923076925, 60611.44230769232, 60808.37423076924, 61037.03230769232, 61275.112307692325, 61566.39192307694, 61677.885384615394, 61874.63230769232, 61991.348461538466, 62074.66615384615, 62140.311923076915, 62269.976153846146, 62377.66769230769, 62546.71115384615, 62559.91692307691, 62642.00461538461, 62734.1073076923, 62686.4723076923, 62595.312307692315, 62495.54692307693, 62345.59730769232, 62222.135384615394, 61852.915384615386, 61462.19115384615, 61182.31961538463, 61028.50192307693, 60787.03576923079, 60539.14000000001, 60195.099615384606, 59832.22384615383, 59616.988846153836, 59238.99615384614, 58753.06346153845, 58212.53653846153, 57714.80615384614, 57319.73576923076, 56684.939230769225, 55855.920000000006, 55093.39384615386, 54357.26307692309, 53683.135384615394, 52932.26961538462, 52040.31423076924, 51293.57076923076, 50583.33115384616, 49783.56384615384, 49096.6426923077, 48541.61692307692]

Implementing Exponential Moving Average (EMA)

In this section, we are going to implement an algorithm for what is called the “exponential moving average”. This is similar to the SME, however, more importance is put on recent numbers. The goal here is to make the algorithm more responsive to recent price movements. Like SME, the EMA is used in an attempt to discover trend changes.

The EMA is also used as a basis for a different technical indicator we will look at: the moving average convergence divergence (MACD) indicator.

The Exponential Moving Average formula

Here is a quick explanation of the EMA formula:

   

These symbols have the following meaning:

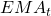• : Today’s EMA.
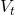• : Today’s price value.
• : Smoothing factor. It is recommended to use 2 as the value.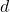
• : Number of time units (usually days) in the time window.
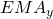• : Yesterday’s EMA

We should note that for the first day in the sequence there is no EMA from the day before. Instead, we use an SMA calculation to get the first “EMA”. This will become more clear when we look at the test setup and results in the next section.

The EMA function we are going to implement has the same parameters as the SMA:

1. A data set, or list, of floating point values.
2. The window size (number of values to use) for calculating the average.

Writing the Exponential Moving Average tests

We are going to start by writing a test function this time as well. We can see the results being a bit different from the SMA because the more recent prices weigh more. However, when there is only 1 result, it is the same as it would be for SMA. That is because as mentioned the first EMA is actually an SMA calculation.

#[test]
fn test_exponential_moving_average() {
    let data_set = vec![5.0, 6.0, 4.0, 2.0];

    let result = exponential_moving_average(&data_set, 2).unwrap();
    assert_eq!(3, result.len());
    assert_eq!(vec![5.5, 4.5, 2.8333333333333335], result);

    let result = exponential_moving_average(&data_set, 4).unwrap();
    assert_eq!(1, result.len());
    assert_eq!(vec![4.25], result);

    let result = exponential_moving_average(&data_set, 5);
    assert_eq!(None, result);

    let data_set = vec![
        22.27, 22.19, 22.08, 22.17, 22.18, 22.13, 22.23, 22.43, 22.24, 22.29, 22.15, 22.39,
    ];

    let result = exponential_moving_average(&data_set, 10).unwrap();
    assert_eq!(3, result.len());
    assert_eq!(
        vec![22.220999999999997, 22.208090909090906, 22.241165289256195],
        result
    );
}

Writing the Exponential Moving Average algorithm

In this section, we will write the actual Rust code for another one of the technical indicators, at the end we will apply it to Binance data. This function will be quite different from the simple_moving_average function.

Here is the code for this algorithm:

pub fn exponential_moving_average(data_set: &Vec<f64>, window_size: usize) -> Option<Vec<f64>> {
    if window_size > data_set.len() {
        return None;
    }

    let mut result: Vec<f64> = Vec::new();

    let weighted_multiplier = 2.0 / (window_size as f64 + 1.0);
    let first_slice = &data_set[0..window_size];
    let first_sma: f64 = first_slice.iter().sum::<f64>() / window_size as f64;
    result.push(first_sma);
    for i in window_size..data_set.len() {
        let previous_ema = result[result.len() - 1];
        let ema: f64 =
            (data_set[i] * weighted_multiplier) + previous_ema * (1.0 - weighted_multiplier);
        result.push(ema);
    }

    Some(result)
}

The function parameters and return type should look familiar as it is the same as for simple_moving_average.

First, we calculate the weighted multiplier on line 27. This is the part of the formula.

Then we get the first slice of the data set to calculate the SMA for the first step in the sequence.

Our main calculation happens in the loop on lines 31-36. Here we apply the EMA formula on each value following the end of the first window. So if we have [5.0, 6.0, 4.0, 2.0] and the window size is 2 then SMA will be calculated for [5.0, 6.0], then EMA can be calculated for [6.0, 4.0] and [4.0, 2.0].

Here previous_ema is , ema is , data_set[i] is , and weighted_multiplier is as was mentioned before.

We push the calculated EMA value onto a Vec and at the end return that list.

Executing Exponential Moving Average tests

Now that we have implemented the EMA algorithm in our function we can run the tests to verify the validity with our tests. Let’s run them using the cargo test command. The result should look like this:

running 2 tests
test test_statistics::test_statistics::test_exponential_moving_average ... ok
test test_statistics::test_statistics::test_simple_moving_average ... ok

test result: ok. 2 passed; 0 failed; 0 ignored; 0 measured; 0 filtered out; finished in 0.00s

Exponential Moving Average with real data

Now we can see what our second of the technical indicators written in Rust looks like with real price data from Binance. We will calculate the EMA for a window of 26 days, so we can compare the values to the results from the SMA.

We can pass the same data set as one we used for the SMA calculation:

let result = statistics::exponential_moving_average(&price_data, 26);

let ema_data = match result {
    Some(data) => data,
    _ => panic!("Calculating EMA failed"),
};

println!("EMA: {:?}", ema_data);

After running the program the result looks like this:

EMA: [49070.09730769231, 49619.00417378917, 50179.37942017516, 50680.948352014035, 51206.526251864845, 51656.033936911896, 51883.07068232583, 52019.62322437577, 52533.75187442201, 52874.82877261297, 53220.49108575275, 53444.69026458588, 53828.19617091285, 54263.70089899338, 54544.33342499387, 54718.20650462396, 55134.99639317033, 55499.72777145401, 56100.24719579075, 56797.93999610255, 57359.57407046532, 57860.511546727146, 58372.641061784394, 58854.847649800366, 59454.315231296634, 60052.20521416355, 60290.826309410695, 60378.21769389879, 60419.6178647211, 60491.86913400102, 60669.988457408355, 60858.87746056329, 60862.7465375586, 60895.12086810982, 60966.53339639798, 61061.87981147961, 61025.880566184824, 60832.36645017114, 60795.06597238069, 60964.22997442656, 60955.932939283855, 60980.43790674431, 60958.792135874355, 61050.22605173552, 61416.980418273626, 61629.09964654966, 61657.30263569413, 61647.74910712419, 61590.55065474462, 61596.61505068946, 61281.89838026802, 60991.90590765558, 60621.90769227368, 60388.53304840155, 59964.1231929644, 59592.68591941148, 59174.81511056618, 58775.58584311684, 58519.24615103411, 57997.22717688343, 57347.428126743915, 56669.84159883696, 56000.58666558978, 55418.440245916456, 54559.600227700415, 53594.02095157446, 52663.09643664302, 51884.15225615094, 51237.985422361984, 50603.36724292776, 50026.12300271089, 49643.836854361936, 49191.96819848327, 48565.480183780805, 48154.37942942667]

The downtrend at the end there is a bit more pronounced thanks to the weight that is applied to recent prices.

Implementing Moving Average Convergence Divergence (MACD)

The well-known MACD indicator is the third of the technical indicators we will implement in Rust and apply on Binance data. This is another trend-following indicator. The MACD indicator shows the relationship between two moving averages. The result is a MACD line and a signal line. The signal line is a 9 day EMA of the MACD line. If the lines cross this could indicate a buy or sell signal. More information on investopedia.com.

The Moving Average Convergence Divergence formula

The formula for the MACD line is simply:

   

Then to get the signal line we apply a 9 day EMA calculation on the results from the MACD calculation. We should note that these numbers (12 day EMA, 26 day EMA, 9 day EMA) are what is commonly used for the MACD indicator. However, other values can be used as well, according to your preference. In the Binance trading dashboard, these values are called “fast length”, “slow length”, and “signal length” respectively.

So, the input parameters for our MACD function is:

• A data set Vec<f64>
• the fast length of the time window
• slow length of the time window
• finally, the signal length

Writing the Moving Average Convergence Divergence tests

Let’s write some tests again too, add to test_statistics.rs:

#[test]
fn test_moving_average_convergence_divergence() {
    let data_set = vec![
        5.0, 6.0, 4.0, 2.0, 1.5, 1.0, 2.0, 3.0, 3.5, 3.5, 4.0, 4.5, 5.0,
    ];

    let result = moving_average_convergence_divergence(&data_set, 12, 26, 9);
    assert_eq!(None, result);

    let result = moving_average_convergence_divergence(&data_set, 3, 6, 2).unwrap();
    assert_eq!(8, result.macd.len());
    assert_eq!(
        vec![
            -1.5,
            -1.0178571428571432,
            -0.48596938775510257,
            -0.1194424198250732,
            0.02852327155351908,
            0.18443626539537084,
            0.32091429671097904,
            0.4309544083649852
        ],
        result.macd
    );
    assert_eq!(7, result.signal.len());
    assert_eq!(
        vec![
            -1.2589285714285716,
            -0.7436224489795923,
            -0.32750242954324627,
            -0.09015196214540272,
            0.09290685621511298,
            0.24491181654569036,
            0.36894021109188696
        ],
        result.signal
    );
}

We should note here that the result is a struct containing two Vec<f64>, one for macd and one for signal.

The first test on lines 62 and 63 tests that None is returned if one of the “lengths” is longer than the data set length. Then we test a normal situation with correct inputs.

Writing the Moving Average Convergence Divergence algorithm

We are not only going to write a function in this section but also a small struct containing the MACD and signal values. Let’s open up the statistics.rs source file and add some code.

First, the struct. Let’s just add it to statistics.rs:

#[derive(PartialEq, Debug)]
pub struct MACD {
    pub macd: Vec<f64>,
    pub signal: Vec<f64>,
}

Here we see a simple struct with two fields of Vec<f64>. The struct annotation #[derive(PartialEq, Debug)] is there to return the struct wrapped in Some and do a comparison with None (see tests).

Next, let’s move on to the function moving_average_convergence_divergence:

pub fn moving_average_convergence_divergence(
    data_set: &Vec<f64>,
    fast_length: usize,
    slow_length: usize,
    signal_length: usize,
) -> Option<MACD> {
    let fast_ema_result = exponential_moving_average(data_set, fast_length);
    let slow_ema_result = exponential_moving_average(data_set, slow_length);

    let (fast_ema, slow_ema) = match (fast_ema_result, slow_ema_result) {
        (Some(fast_ema), Some(slow_ema)) => (fast_ema, slow_ema),
        _ => return None,
    };

    let mut macd: Vec<f64> = Vec::new();
    for i in 0..slow_ema.len() {
        let macd_val = fast_ema[(fast_ema.len() - slow_ema.len()) + i] - slow_ema[i];
        macd.push(macd_val);
    }

    let signal_result = exponential_moving_average(&macd, signal_length);
    let signal = match signal_result {
        Some(signal) => signal,
        _ => return None,
    };

    Some(MACD { macd, signal })
}

This algorithm is fairly simple as it uses the EMA function a couple of times and just subtracts one set of numbers from the other.

On lines 53 and 54 we get the EMA results for the fast and slow time windows. Then make sure the results are both valid on lines 56 – 59, otherwise we return None.

Then loop through the shortest Vec, which is slow_ema in this case. Because the slow EMA works with a bigger time window length, it will have fewer values in the resulting Vec.

We line up the numbers from slow_ema with fast_ema using fast_ema[(fast_ema.len() - slow_ema.len()) + i]. Let’s say we have fast_ema = [1,2,3,4,5,6,7,8] and slow_ema = [11,12,13] we should take only a portion from fast_ema. Namely: [6, 7, 8]. So, fast_ema.len() is 8 and slow_ema.len() is 3, 8-3 = 5, and because the index starts at 0 this gives us 6 in the first iteration of the loop. Which is what we wanted.

Then we subtract the slow_ema value from the fast_ema one and add it to the macd vector.

Finally, we run an EMA calculation on the macd, which will be the signal line values, and then return both macd and signal as parts of the MACD struct.

Executing the Moving Average Convergence Divergence tests

That is number three of our technical indicators Rust implementations, let’s run the test and then apply it to Binance coin price data.

The test results should look like this:

running 3 tests
test test_statistics::test_statistics::test_exponential_moving_average ... ok
test test_statistics::test_statistics::test_simple_moving_average ... ok
test test_statistics::test_statistics::test_moving_average_convergence_divergence ... ok

test result: ok. 3 passed; 0 failed; 0 ignored; 0 measured; 0 filtered out; finished in 0.00s

Moving Average Convergence Divergence with real data

Finally, let’s look at real Binance price data with this technical indicator as well:

let result = statistics::moving_average_convergence_divergence(&price_data, 12, 26, 9);

let macd_data = match result {
    Some(data) => data,
    _ => panic!("Calculating MACD failed"),
};

println!("MACD: {:?}", macd_data);

And the result in the terminal:

MACD: MACD { macd: [821.6988331526445, 1286.7311318874345, 1692.5470795356305, 1972.5781829120242, 2235.3632561224513, 2375.7794444654064, 2254.9917920906228, 2055.326346018177, 2292.98428603528, 2307.7023383445776, 2325.08152646901, 2208.9687932164306, 2282.2697709448476, 2400.282334453499, 2333.344344787016, 2161.7241609196935, 2278.1018042040523, 2320.504780518524, 2610.302955345891, 2960.158699665386, 3109.6598247058355, 3170.7897679745, 3234.563031014346, 3256.2956669456835, 3400.961570687381, 3521.6682295085193, 3236.8959738326594, 2833.068639911893, 2441.836413735662, 2144.0150808199687, 2006.021442999183, 1900.8531917948712, 1612.6101096057973, 1399.4079214564554, 1261.0452051405227, 1169.7421629540695, 951.0348545407105, 596.3418367861887, 464.44557687269116, 575.1860504233919, 477.77638097823365, 430.6768806325563, 341.12158115224156, 387.1211433126591, 722.5418698678259, 839.828400703147, 741.0064131729523, 616.7262074080063, 460.2554341459254, 395.98567806713254, -3.8535402631750912, -315.5535142796434, -665.46017752013, -814.4024330216998, -1146.161152482804, -1369.8330705508197, -1609.0996380337237, -1791.480799018529, -1791.9225542172353, -2078.4127891539174, -2458.43718645013, -2809.921518389325, -3098.359083089388, -3248.6126841154837, -3673.728266866805, -4148.3916064370205, -4512.70947525771, -4657.307469629966, -4636.66877610817, -4606.768389148252, -4519.680867864583, -4236.03667463248, -4070.9651651243403, -4119.340989126511, -3928.3189596225056], signal: [1887.5555946910745, 1971.5849434217753, 2042.2842600312224, 2075.6211666682643, 2116.950887523581, 2173.617176909565, 2205.5626104850553, 2196.7949205719833, 2213.056297298397, 2234.5459939424227, 2309.6973862231166, 2439.7896489115706, 2573.7636840704236, 2693.168900851239, 2801.447726883861, 2892.417314896226, 2994.1261660544574, 3099.63457874527, 3127.086857762748, 3068.2832141925774, 2942.9938541011943, 2783.1980994449495, 2627.7627681557965, 2482.3808528836116, 2308.426704228049, 2126.6229476737303, 1953.507399167089, 1796.754351924485, 1627.61045244773, 1421.356729315422, 1229.9744988268758, 1099.0168091461792, 974.7687235125902, 865.9503549365835, 760.9846001797151, 686.211908806304, 693.4779010186085, 722.7480009555162, 726.3996833990035, 704.4649882008041, 655.6230773898284, 603.6955975252893, 482.1857699675964, 322.63791311814845, 125.01829499049279, -62.865850611945746, -279.52491098611745, -497.5865428990579, -719.8891619259912, -934.2074893444988, -1105.750502319046, -1300.2829596860204, -1531.9138050388424, -1787.5153477089389, -2049.6840947850287, -2289.46981265112, -2566.321503494257, -2882.7355240828097, -3208.73031431779, -3498.4457453802256, -3726.0903515258146, -3902.2259590503027, -4025.716940813159, -4067.7808875770233, -4068.4177430864866, -4078.6023922944914, -4048.5457057600947] }

Implementing Bollinger Bands (BOLL)

Next up in our lineup of technical indicators that we will implement in Rust and use with Binance price data, is Bollinger Bands.

Bollinger bands are a set of 2 trendlines plotted 2 standard deviations away above and below a simple moving average line. The goal is to help determine when an asset is oversold or overbought.

The Bollinger Bands formula

Symbols explanation:

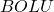• : Upper Bollinger Band
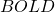• : Lower Bollinger Band
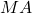• : Moving average
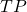• : Typical price =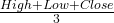
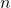• : Number of days in smoothing period (recommended 20)
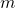• : Number of standard deviations (recommended 2)
• : Standard Deviation over last 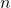periods of TP

For more information about Bollinger Bands please see the investopedia.com article.

Writing the Bolling Bands tests

Below is a listing of the tests we should add to test_statistics.rs for the Bollinger bands function. As with the result for the MACD function, the Bollinger bands function also returns a struct. In this case a struct with three Vec<f64> fields: representing the upper bound, middle bound, and lower bound values. The middle bound represents the moving average running between the bands.

#[test]
fn test_bollinger_bands() {
    let data_set = vec![
        5.0, 6.0, 4.0, 2.0, 1.5, 1.0, 2.0, 3.0, 3.5, 3.5, 4.0, 4.5, 5.0,
    ];

    let result = bollinger_bands(&data_set, 20, 2.0);
    assert_eq!(None, result);

    let result = bollinger_bands(&data_set, 8, 2.0).unwrap();

    assert_eq!(6, result.middle_bound.len());
    assert_eq!(
        vec![3.0625, 2.875, 2.5625, 2.5625, 2.875, 3.3125],
        result.middle_bound
    );

    assert_eq!(6, result.upper_bound.len());
    assert_eq!(
        vec![
            6.395572906493346,
            5.906088913245535,
            4.589659342528357,
            4.589659342528357,
            5.206844763272204,
            5.758798223847616
        ],
        result.upper_bound
    );

    assert_eq!(6, result.lower_bound.len());
    assert_eq!(
        vec![
            -0.27057290649334576,
            -0.1560889132455352,
            0.535340657471643,
            0.535340657471643,
            0.5431552367277961,
            0.8662017761523844
        ],
        result.lower_bound
    );
}

Writing the Bollinger Bands algorithm

Let’s write the code for the Bollinger Bands algorithm to make the tests succeed.

First, we will add the BollingerBands struct to statistics.rs:

#[derive(PartialEq, Debug)]
pub struct BollingerBands {
    pub upper_bound: Vec<f64>,
    pub middle_bound: Vec<f64>,
    pub lower_bound: Vec<f64>,
}

This is similar to the MACD struct but with different names for the fields. Nothing more to say here.

Next, we’ll write the function:

pub fn bollinger_bands(
    data_set: &Vec<f64>,
    window_size: usize,
    multiplier: f64,
) -> Option<BollingerBands> {
    let middle_bound_result = simple_moving_average(data_set, window_size);

    let middle_bound = match middle_bound_result {
        Some(middle_bound) => middle_bound,
        _ => return None,
    };

    let mut upper_bound: Vec<f64> = Vec::new();
    let mut lower_bound: Vec<f64> = Vec::new();

    for i in 0..middle_bound.len() {
        let slice = &data_set[i..window_size + i];
        let variance = slice
            .iter()
            .map(|value| {
                let diff = middle_bound[i] - (*value as f64);
                diff * diff
            })
            .sum::<f64>()
            / window_size as f64;

        let standard_deviation = variance.sqrt();

        upper_bound.push(middle_bound[i] + multiplier * standard_deviation);
        lower_bound.push(middle_bound[i] - multiplier * standard_deviation);
    }

    Some(BollingerBands {
        upper_bound,
        middle_bound,
        lower_bound,
    })
}

Our functions parameters are mostly familiar: pub fn bollinger_bands(data_list: &Vec<f64>, window_size: usize, multiplier: f64) -> Option<BollingerBands>. However, the multiplier is different. This multiplier is the number of standard deviations the upper and lower bands should be away from the middle band, or the simple moving average. Typically this has a value of 2. Also, we should remember to pass in a Vec<f64> of the “typical price” for data_set.

On lines 88-93 we calculate the SMA of the typical price vector and store it in the middle_bound variable after checking for None.

Then we loop through the length of the middle_bound vector and calculate the variance by subtracting the typical price value (data_list[i]) from the average (middle_bound[i]), then squaring that difference and dividing by the window size.

Next, taking the square root of the variance gives us the standard deviation on line 109.

With the standard deviation calculated, we can calculate the upper and lower bands on lines 111 and 112.

Finally, a new instance of the BollingerBands struct is created and returned with the calculated bands.

Running the Bollinger Bands tests

We can now run the test to verify the results:

running 4 tests
test test_statistics::test_statistics::test_bollinger_bands ... ok
test test_statistics::test_statistics::test_exponential_moving_average ... ok
test test_statistics::test_statistics::test_simple_moving_average ... ok
test test_statistics::test_statistics::test_moving_average_convergence_divergence ... ok

test result: ok. 4 passed; 0 failed; 0 ignored; 0 measured; 0 filtered out; finished in 0.00s

Bollinger Bands with real data

In this last section for the Bollinger Bands chapter is we will see how to use it with Binance price data.

First, we have to create a new Vec<f64> that represents the “typical price” per day. Which is the average of the high, low, and close prices. This is a small adjustment to the price_data calculation we wrote earlier. See lines 49-45:

let typical_price_data: Vec<f64> = kline_data
    .iter()
    .rev()
    .take(100)
    .map(|f| (f.high + f.low + f.close) / 3.0)
    .collect();
let result = statistics::bollinger_bands(&typical_price_data, 20, 2.0);

let boll_data = match result {
    Some(data) => data,
        _ => panic!("Calculating BOLL failed"),
    };

    println!("BOLL: {:?}", boll_data);

The result:

BOLL: BollingerBands { upper_bound: [51449.18249532616, 51595.74807049559, 51549.082757447155, 51403.73245984006, 51183.38207161313, 50798.53533498869, 52075.1461891192, 53892.02735073466, 55596.847818591385, 56869.95979533894, 58043.73613895038, 58638.031095246246, 58891.46915348812, 59297.38863261007, 60157.89832228698, 60571.60540491717, 60860.55576315069, 61235.15643654648, 61745.04002416486, 62034.629373403746, 61996.65096533305, 62113.84232404656, 62462.38484300772, 62627.415949531845, 63303.93418465342, 63496.736356599205, 64319.58211792683, 65054.313570283644, 65884.76095012785, 66758.43125124583, 67878.93484379316, 68549.58691432544, 68448.3011405848, 68246.94309682012, 68257.93559265525, 68146.2644289038, 68006.84227688503, 67831.58602112901, 67756.77781914736, 67660.24069143334, 67303.26392253971, 66984.32383787305, 66941.7717637773, 67077.92112678086, 66915.54707049325, 66679.41439876491, 66516.70517731474, 66356.73060875118, 66031.06414490796, 65672.57376244695, 65141.2481507637, 64434.57437043949, 64353.54385773597, 64357.969132583436, 64353.39011111, 64345.54374063566, 64627.14648494285, 64917.485058487924, 65300.33315925052, 65436.88317677584, 65647.37817022078, 65765.85318889849, 65927.89224170399, 66112.70668802809, 66113.44654217215, 66190.34299588039, 66625.03263533601, 66819.05771744222, 66748.88964049672, 66217.72767496764, 65434.78818762744, 64938.20295770155, 64426.50158739425, 63599.057519405746, 62435.55391370506, 61140.74601270351, 60186.10982039047, 59212.86969786902, 58259.53727638045, 57027.570951797024, 55823.86105055791], middle_bound: [48628.083999999995, 48703.9195, 48692.695833333346, 48642.121499999994, 48560.86116666667, 48427.485166666665, 48639.932166666666, 49024.05583333333, 49488.168999999994, 50021.37766666666, 50553.39, 51024.21866666667, 51424.68316666667, 51787.96183333335, 52295.4165, 52751.69316666668, 53223.40633333333, 53587.277666666676, 54112.47316666667, 54658.93933333334, 55097.42083333334, 55498.599, 55948.48366666667, 56512.10399999999, 57288.53683333333, 58115.77033333333, 58613.42316666666, 58983.71233333333, 59346.69066666666, 59758.394499999995, 60231.48483333333, 60741.682166666666, 61146.210333333336, 61424.61983333332, 61572.86283333334, 61813.6635, 62078.84650000001, 62359.071333333326, 62452.66166666666, 62565.0775, 62780.3975, 62964.84150000002, 62987.121333333336, 62914.7745, 62748.629166666666, 62628.52133333332, 62447.23183333331, 62292.99199999999, 62125.42999999998, 62027.556, 61940.69766666666, 61799.037666666656, 61743.4935, 61728.97049999998, 61714.80633333333, 61653.09116666665, 61418.412666666656, 61105.02133333334, 60851.72266666667, 60619.63916666666, 60293.120333333325, 59937.984833333336, 59650.88733333333, 59393.638833333345, 59027.09833333333, 58442.78633333333, 57839.27316666666, 57204.59900000001, 56520.95, 55672.39583333335, 54553.94300000001, 53466.932166666666, 52469.463, 51575.890166666664, 50650.172000000006, 49747.311, 49013.76166666667, 48407.114333333346, 47749.67466666667, 46987.14016666667, 46446.516166666675], lower_bound: [45806.98550467383, 45812.09092950442, 45836.30890921954, 45880.51054015993, 45938.34026172021, 46056.434998344645, 45204.71814421413, 44156.08431593201, 43379.490181408604, 43172.79553799438, 43063.04386104962, 43410.40623808709, 43957.89717984522, 44278.53503405663, 44432.93467771302, 44931.780928416185, 45586.256903515976, 45939.39889678687, 46479.90630916848, 47283.24929326294, 48198.190701333624, 48883.35567595344, 49434.582490325614, 50396.79205046814, 51273.13948201324, 52734.80431006745, 52907.26421540649, 52913.111096383014, 52808.620383205474, 52758.35774875416, 52584.034822873495, 52933.7774190079, 53844.11952608188, 54602.29656984652, 54887.79007401143, 55481.062571096205, 56150.85072311499, 56886.55664553764, 57148.54551418596, 57469.91430856665, 58257.531077460284, 58945.35916212699, 59032.47090288937, 58751.62787321915, 58581.71126284008, 58577.62826790173, 58377.75848935187, 58229.25339124879, 58219.795855091994, 58382.538237553046, 58740.14718256962, 59163.50096289382, 59133.44314226403, 59099.97186741653, 59076.222555556655, 58960.63859269764, 58209.67884839046, 57292.55760817875, 56403.11217408282, 55802.39515655748, 54938.86249644587, 54110.116477768184, 53373.88242496268, 52674.57097863859, 51940.750124494494, 50695.22967078627, 49053.5136979973, 47590.140282557804, 46293.01035950326, 45127.06399169906, 43673.09781237257, 41995.66137563178, 40512.42441260576, 39552.72281392758, 38864.790086294954, 38353.875987296495, 37841.413512942876, 37601.35896879767, 37239.8120569529, 36946.70938153632, 37069.17128277544] }

That is a lot of numbers.

Implementing Relative Strength Index (RSI)

The last of the technical indicators we are going to implement in Rust and use with Binance coin price data is the Relative Strength Index indicator.

This indicator is a momentum indicator. It is used to measure the magnitude of recent price changes to analyze if assets are oversold or overbought. The RSI is plotted as a line graph moving between a value of 0 or 100. The common way to read the indicator is that values of 70 or above indicate overbought, and 30 or below indicate an oversold asset.

You can read more detailed information about this indicator on investopedia.com here.

The Relative Strength Index formula

There is a two-part calculation for the RSI indicator. The first part is:

   

With the average gain or loss being expressed in percentage gain or loss over a past time window. The time window typically is 14 periods (days). The average loss should be expressed as a positive value for the calculation to work. A period with a “loss” means 0 gain and vice versa, a period that had a “gain” means a 0 for the loss in the calculation.

The second step of the calculation smooths the results:

   

Writing the Relative Strength Index tests

The last test we will write in this tutorial. It just has to test the validity of one vector that is returned by the function. Of course, we also test for the regular, “what if the window size is bigger than the data set”, handling code:

#[test]
fn test_relative_strength_index() {
    let data_set = vec![
        5.0, 6.0, 4.0, 2.0, 1.5, 1.0, 2.0, 3.0, 3.5, 3.5, 4.0, 4.5, 5.0,
    ];

    let result = relative_strength_index(&data_set, 14);
    assert_eq!(None, result);

    let result = relative_strength_index(&data_set, 8).unwrap();

    assert_eq!(5, result.len());
    assert_eq!(
        vec![
            56.852791878172596,
            56.852791878172596,
            59.17295654731064,
            61.256328819550575,
            63.16578540011347
        ],
        result
    );

    let data_set = vec![
        44.34, 44.09, 44.15, 43.61, 44.33, 44.83, 45.10, 45.42, 45.84, 46.08, 45.89, 46.03,
        45.61, 46.28, 46.28, 46.00, 46.03,
    ];

    let result = relative_strength_index(&data_set, 14).unwrap();

    assert_eq!(3, result.len());
    assert_eq!(
        vec![70.53539393736207, 66.436571546019, 66.66146763681454],
        result
    );
}

Writing the Relative Strength Index algorithm

The code for the Relative Strength Index is a relatively long function, so we will go through it piece by piece. However, let’s look at the whole thing first.

Let’s open statistics.rs and add the following:

pub fn relative_strength_index(data_set: &Vec<f64>, window_size: usize) -> Option<Vec<f64>> {
    let mut result: Vec<f64> = Vec::new();

    if window_size > data_set.len() {
        return None;
    }

    let mut previous_average_gain;
    let mut previous_average_loss;

    // RSI Step one
    let mut gains_sum = 0.0;
    let mut loss_sum = 0.0;
    for i in 0..(window_size + 1) {
        let gain = if i == 0 {
            0.0
        } else {
            (100.0 / data_set[i - 1]) * data_set[i] - 100.0
        };

        if gain >= 0.0 {
            gains_sum += gain;
        } else {
            loss_sum += gain.abs();
        }
    }
    let current_average_gain = gains_sum / window_size as f64;
    let current_average_loss = loss_sum / window_size as f64;

    let rsi_a = 100.0 - 100.0 / (1.0 + (current_average_gain / current_average_loss));
    previous_average_gain = current_average_gain;
    previous_average_loss = current_average_loss;

    result.push(rsi_a);

    // RSI Step two
    for i in (window_size + 1)..data_set.len() {
        let gain = (100.0 / data_set[i - 1]) * data_set[i] - 100.0;
        let (current_gain, current_loss) = if gain > 0.0 {
            (gain, 0.0)
        } else {
            (0.0, gain.abs())
        };

        let current_average_gain = (previous_average_gain * (window_size as f64 - 1.0)
            + current_gain)
            / window_size as f64;
        let current_average_loss = (previous_average_loss * (window_size as f64 - 1.0)
            + current_loss)
            / window_size as f64;

        previous_average_gain = current_average_gain;
        previous_average_loss = current_average_loss;

        let rsi = 100.0 - 100.0 / (1.0 + current_average_gain / current_average_loss);
        result.push(rsi);
    }

    Some(result)
}

RSI Algorithm step one

The first part is just the function signature definition and some initializations:

pub fn relative_strength_index(data_set: &Vec<f64>, window_size: usize) -> Option<Vec<f64>> {
    let mut result: Vec<f64> = Vec::new();

    if window_size > data_set.len() {
        return None;
    }

The parameters are the same as for SMA and EMA: a data set of floats and a window size number.

Then we get the implementation of the first step of the RSI formula:

    let mut previous_average_gain;
    let mut previous_average_loss;

    // RSI Step one
    let mut gains_sum = 0.0;
    let mut loss_sum = 0.0;
    for i in 0..(window_size + 1) {
        let gain = if i == 0 {
            0.0
        } else {
            (100.0 / data_set[i - 1]) * data_set[i] - 100.0
        };

        if gain >= 0.0 {
            gains_sum += gain;
        } else {
            loss_sum += gain.abs();
        }
    }
    let current_average_gain = gains_sum / window_size as f64;
    let current_average_loss = loss_sum / window_size as f64;

    let rsi_a = 100.0 - 100.0 / (1.0 + (current_average_gain / current_average_loss));
    previous_average_gain = current_average_gain;
    previous_average_loss = current_average_loss;

    result.push(rsi_a);

First, on lines 129 and 130 we declare 2 variables for tracking the previous gain and previous loss respectively. We need these values for every turn of the loop in the RSI step two calculation. It will be updated every loop with the new average gain and loss. However, before we can do step two we have to calculate the first RSI.

To do that, we need to sum up the gains and losses, expressed as a positive percentage, in the first time window.

We loop through the numbers that fall in the time window with for i in 0..(window_size+1). For the first value, there is no previous value to calculate a gain or loss from, so we set it to 0 on lines 136 and 137. Otherwise, we calculate the gain/loss percentage with (100.0 / data_set[i - 1]) * data_set[i] - 100.0. Then depending on if the number is positive or negative we add it to the sum of gain or loss respectively. Before adding to loss_sum we turn the number positive using .abs() on line 145.

On lines 148 and 149 we calculate the average by dividing by the time window size.

Next, we can plug these numbers into the RSI step one formula on line 151.

Finally, we set the variables tracking the previous average gain and average loss values with the ones we just calculated. We also push the RSI from step one into our result vector.

RSI algorithm step two

This is step two and the final step for calculating the Relative Strength Index:

    // RSI Step two
    for i in (window_size + 1)..data_set.len() {
        let gain = (100.0 / data_set[i - 1]) * data_set[i] - 100.0;
        let (current_gain, current_loss) = if gain > 0.0 {
            (gain, 0.0)
        } else {
            (0.0, gain.abs())
        };

        let current_average_gain = (previous_average_gain * (window_size as f64 - 1.0)
            + current_gain)
            / window_size as f64;
        let current_average_loss = (previous_average_loss * (window_size as f64 - 1.0)
            + current_loss)
            / window_size as f64;

        previous_average_gain = current_average_gain;
        previous_average_loss = current_average_loss;

        let rsi = 100.0 - 100.0 / (1.0 + current_average_gain / current_average_loss);
        result.push(rsi);
    }

    Some(result)
}

We loop through the remaining values in the data set, after the initial time window we used for RSI step one. Then, the first part in the loop where the current gain and loss are calculated looks similar to RSI step one. However, we don’t have to calculate the sum of gains and losses here. We just have to calculate the “current” gain and loss. If there is again (positive number) the loss is set to 0, and the other way around too (lines 160 -163).

Then we calculate the average gain and loss on lines 166 – 177, using the following part formula RSI step two: .

Where the “13” in the formula is represented as window_size - 1.0 in the Rust code. Because 14 is the typical window size it shows window size – 1 = 13 in the formula.

We have to make sure to update the values for previous_average_gain and previous_average_loss as they will be used in the next round of the loop.

Finally, we use the RSI calculation again where we plug in the average gain and average loss values, then push the RSI value into the result vector.

Running the Relative Strength Index tests

Now let’s run the tests to see the results:

running 5 tests
test test_statistics::test_statistics::test_exponential_moving_average ... ok
test test_statistics::test_statistics::test_relative_strength_index ... ok
test test_statistics::test_statistics::test_moving_average_convergence_divergence ... ok
test test_statistics::test_statistics::test_bollinger_bands ... ok
test test_statistics::test_statistics::test_simple_moving_average ... ok

test result: ok. 5 passed; 0 failed; 0 ignored; 0 measured; 0 filtered out; finished in 0.00s

Good! We have five tests succeeding for our five technical indicators implemented in Rust, we can now apply RSI to Binance price data as well.

Relative Strength Index with real data

Using the RSI function with real data is easy since it just needs a simple Vec<f64> as input we can use the one we create at the start:

let result = statistics::relative_strength_index(&price_data, 14);

let rsi_data = match result {
    Some(data) => data,
    _ => panic!("Calculating RSI failed"),
};

println!("RSI: {:?}", rsi_data);

The result looks like this:

RSI: [57.358215093789205, 54.954005662150024, 48.05863335404985, 59.60145786112474, 57.0764639330244, 49.345989961472846, 50.702537412604734, 59.14133606979716, 59.42496413400486, 58.87670076792388, 54.98056818590161, 54.06297338027634, 65.44791558529968, 70.17289376358235, 71.15810790612377, 70.33810289048755, 71.58991165873259, 69.69403820622797, 60.78625223031364, 57.55718068605283, 67.51773634016041, 62.50630309816922, 63.178021433312054, 59.51635537037113, 63.76258232283822, 65.47298647805414, 60.84268377701581, 57.674938584668475, 63.8318330785172, 63.06048208791473, 68.21600536118729, 70.47459845949481, 67.48805704501139, 66.78612618087432, 67.70481295219855, 67.86202885722597, 70.78170803363301, 71.5372473879086, 59.46296806433608, 54.943853149078535, 53.60754165395122, 54.6362741664993, 57.90776773909376, 58.5842637009155, 52.17253098691932, 53.13761129386576, 54.54999740291207, 55.55812437261008, 50.4640696233029, 44.627360395009205, 50.31214890932208, 56.931650583202256, 51.23907310381057, 52.27862231376024, 50.68703430706871, 54.4768338176269, 62.20160011800468, 57.71109609644939, 52.21126137146895, 51.05938515366841, 49.45406373674193, 51.48099095555156, 41.809002579905844, 41.864753910622646, 38.9750933676412, 43.59739723114528, 37.858133019771294, 38.80114860200761, 36.74974285041063, 36.39831521986064, 41.92038455705381, 34.126233109391094, 30.3123993498904, 28.666870121793465, 27.75326014995349, 29.93505725127217, 23.493311833153285, 20.68792258271796, 20.09758948673101, 25.32747793112341, 29.690042442999044, 28.83316423912622, 29.466066682693892, 38.137394874536504, 35.2712140441612, 29.96060406830881]

Conclusion

We learned how to turn formulas for technical indicators into Rust code and how to get Binance coin price data and turn that data into technical indicator data. On top of that, we learned the basics of how to test our functions with unit tests.

We can use these functions to generate information for a dashboard for trading signals, plot them on graphs, etc.

My GitHub repository has the full project here.

A reminder: if you are interested in how to visualize technical indicators with Rust I have a quick article about that here: Plot Candles and SMA with Rust: learn how to.

Please follow me on Twitter to get notified on new Rust programming and data gathering or analysis related articles:

Follow @tmdev82